ReST-MCTS*: LLM Self-Training via Process Reward Guided Tree Search

Abstract

Recent methodologies in LLM self-training mostly rely on LLM generating responses and filtering those with correct output answers as training data. This approach often yields a low-quality fine-tuning training set (e.g., incorrect plans or intermediate reasoning).

In this paper, we develop a reinforced self-training approach, called ReST-MCTS*, based on integrating process reward guidance with tree search MCTS* for collecting higher-quality reasoning traces as well as per-step value to train policy and reward models. ReST-MCTS* circumvents the per-step manual annotation typically used to train process rewards by tree-search-based reinforcement learning: Given oracle final correct answers, ReST-MCTS* is able to infer the correct process rewards by estimating the probability this step can help lead to the correct answer. These inferred rewards serve dual purposes: they act as value targets for further refining the process reward model and also facilitate the selection of high-quality traces for policy model self-training.

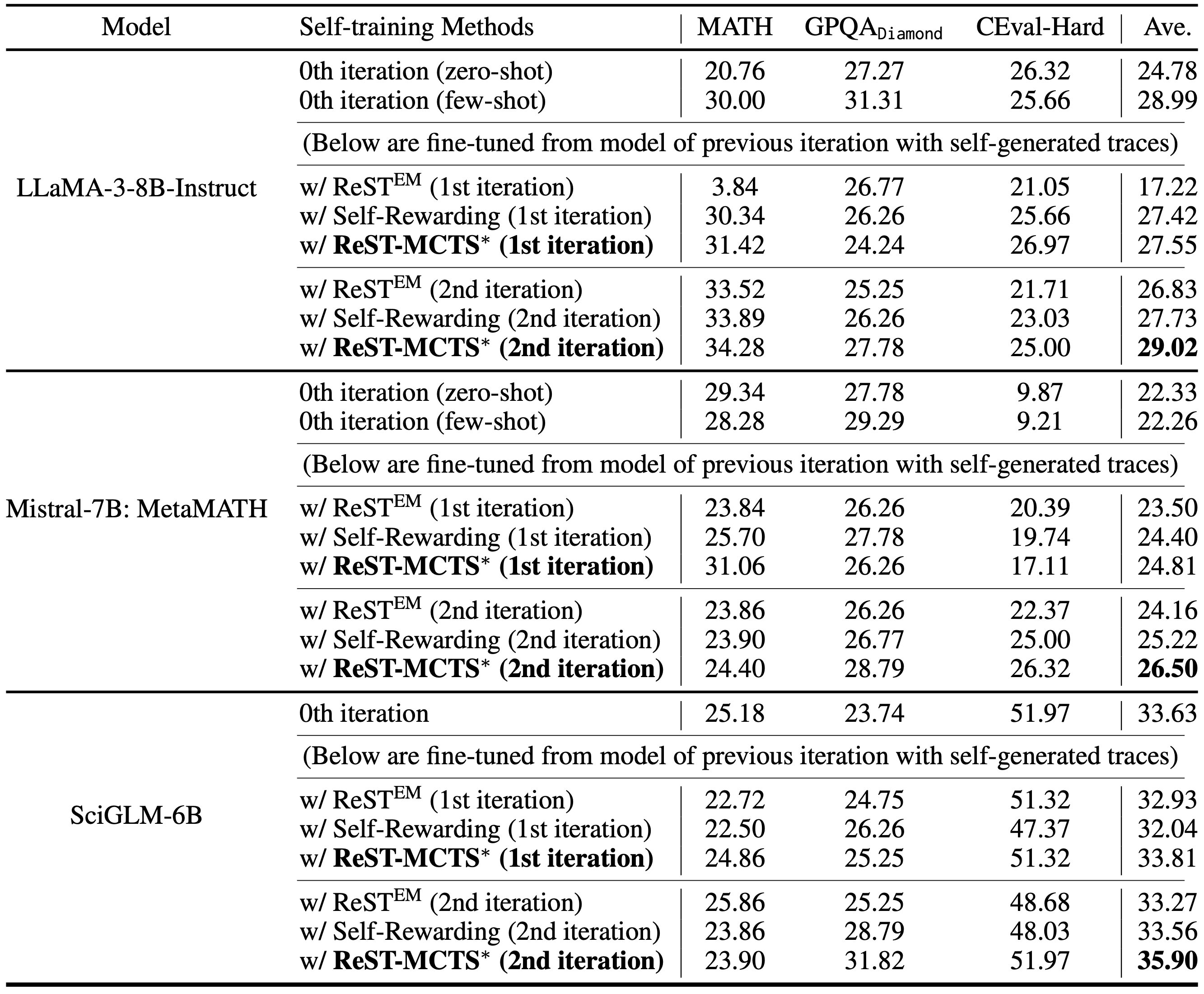
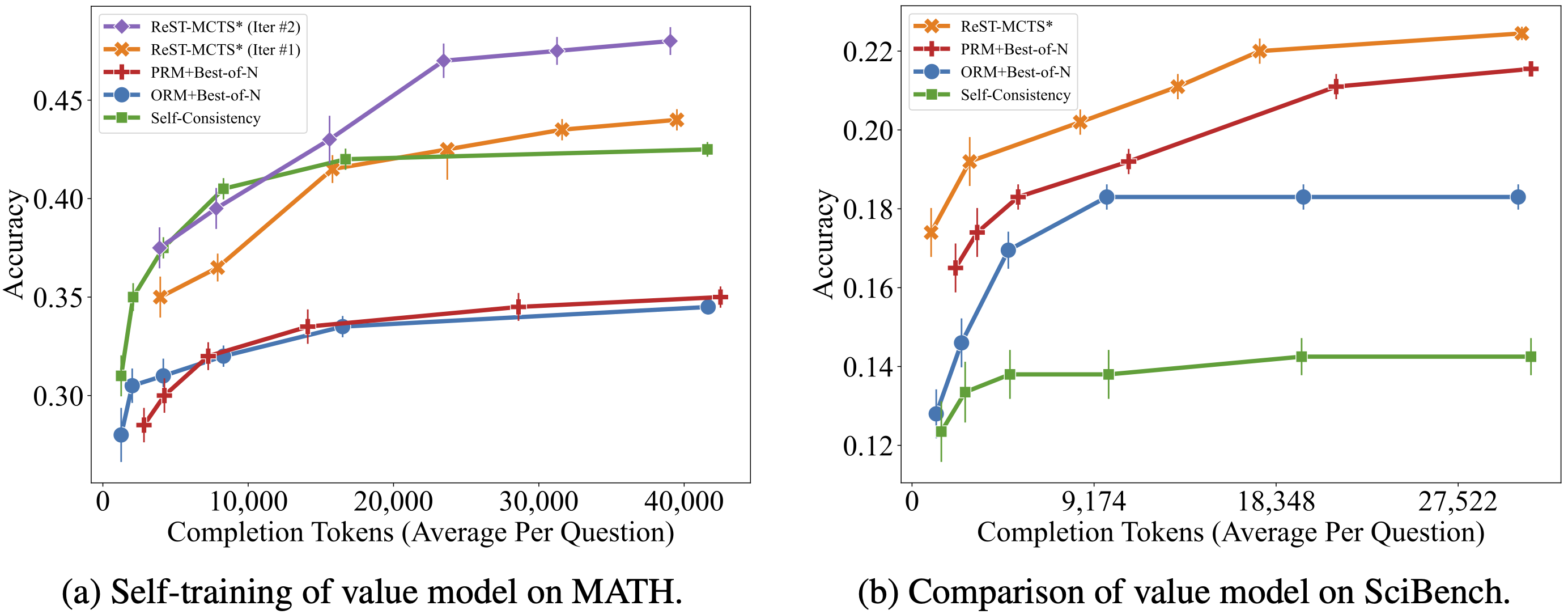
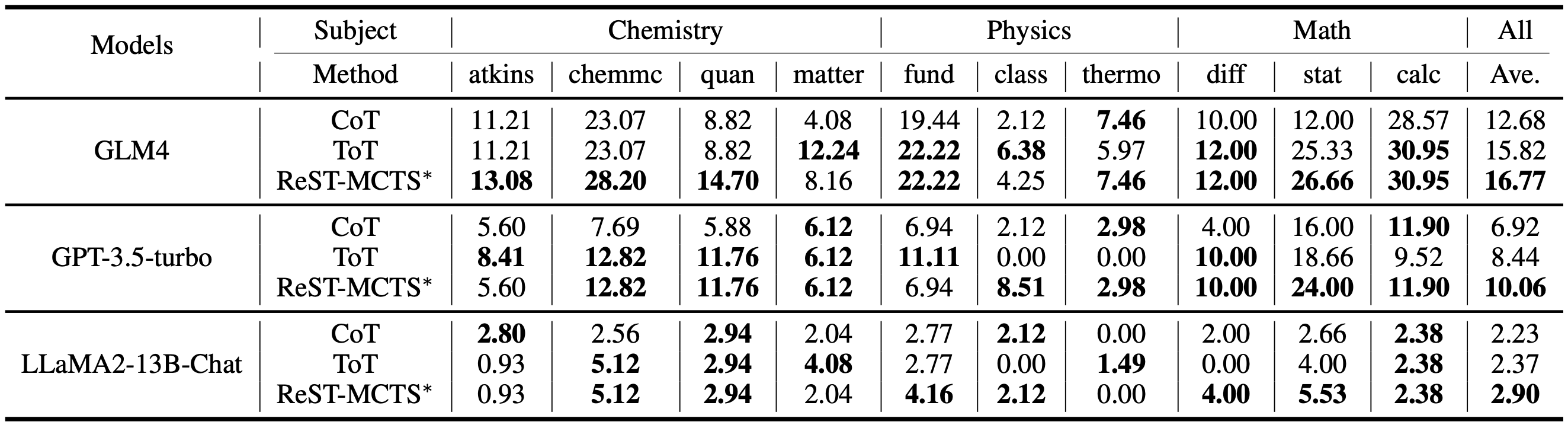
We first show that the tree-search policy in ReST-MCTS* achieves higher accuracy compared with prior LLM reasoning baselines such as Best-of-N and Tree-of-Thought, within the same search budget. We then show that by using traces searched by this tree-search policy as training data, we can continuously enhance the three language models for multiple iterations, and outperform other self-training algorithms such as ReST^EM and Self-Rewarding LM. We release all code at https://github.com/THUDM/ReST-MCTS.

Key Differences

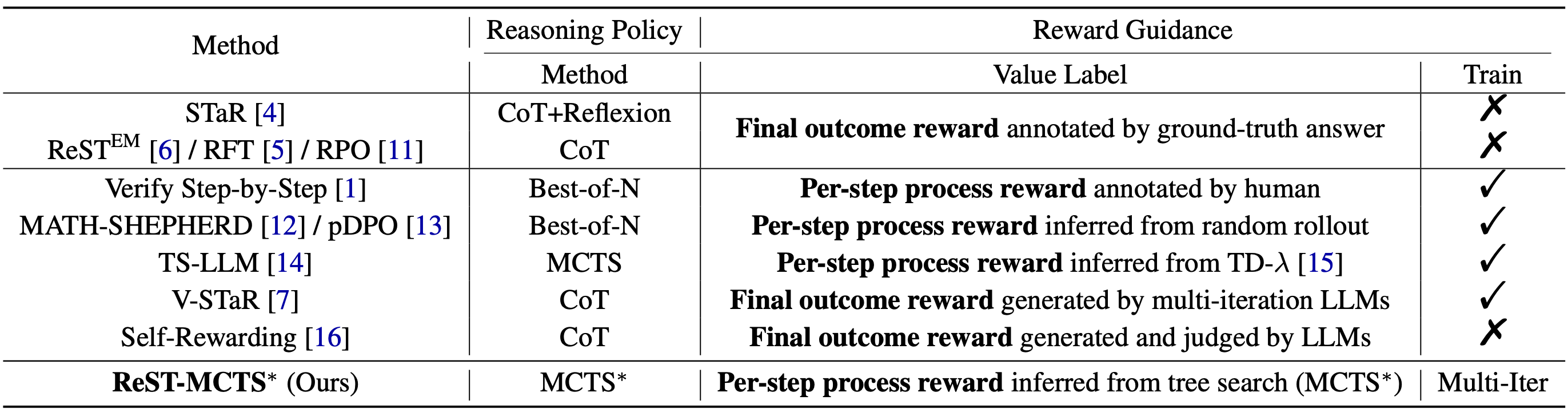
Table 1: Key differences between existing self-improvement methods and our approach. Train refers to whether to train a reward model.

Our Method: ReST-MCTS*

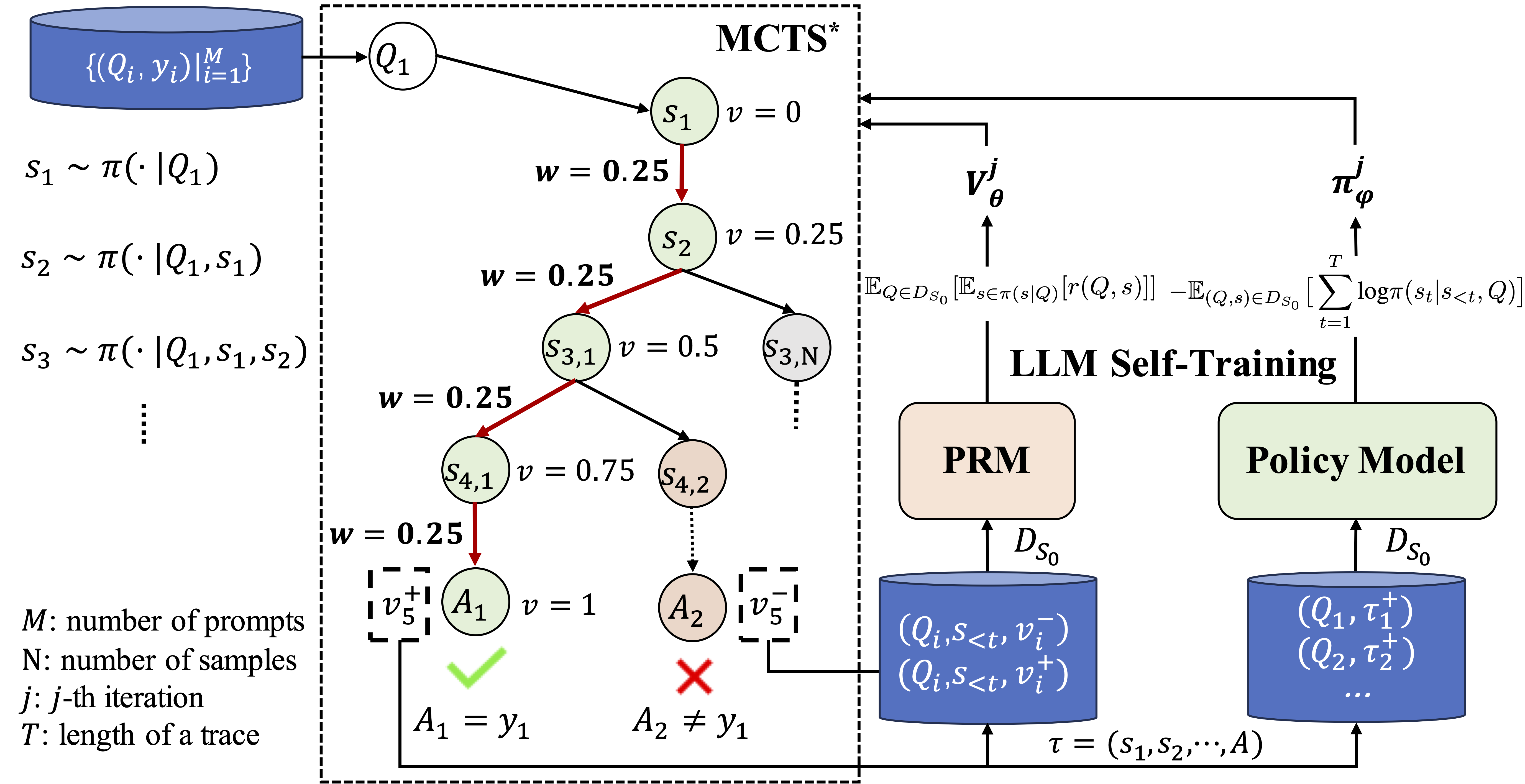
Figure 1: The left part presents the process of inferring process rewards and how we conduct process reward guide tree-search. The right part denotes the self-training of both the process reward model and the policy model.

MCTS* which performs a tree search with sufficient rollout time under the guidance of the PRM.
Process Reward Model (PRM) which evaluates any partial solution's quality and guides MCTS.
Policy Model which generates multiple intermediate reasoning steps for each question.
LLM Self-Training, which uses MCTS* to collect reasoning traces, trains policy model on positive samples, and trains process reward model on all generated traces.

Experimental Results

We validate ReST-MCTS* from three perspectives:

Self-Training approaches which use generated samples and evaluated for multiple iterations, such as ReST^EM and Self-Rewarding, on in-distribution and out-of-distribution benchmarks under three LLM backbones, as shown in Table 2. ReST-MCTS* outperforms existing approaches in each iteration and continuously self-improves by data generated by itself.
Process Reward models which are compared with the state-of-the-art techniques, such as MATH-SHEPHERD (MS) and SC + MS on GSM8K and MATH500, as shown in Table 3. Results indicate ReST-MCTS* learns a good PRM and our reward model implements higher accuracy.
Tree-Search Policy which are compared on college-level scientific reasoning benchmark under three LLMs, such as CoT and ToT, as shown in Table 4. We also evaluated under the same search budget on MATH and SciBench, such as SC and Best-of-N, as shown in Figure 2. Results show the ReST-MCTS* significantly outperforms other baselines despite insufficient budget.

Self-training Results

Table 2: Primary results by training both policy and value model for multiple iterations. For each backbone, different self-training approaches are conducted separately. This means each approach has its own generated train data and corresponding reward (value) model. Our evaluation is zero-shot only, the few-shot baseline only serves as comparison.

Accuracy of Different Verifiers

Table 3: Accuracy of different verifiers on GSM8K test set and MATH500. SC: Self-Consistency, MS: MATH-SHEPHERD. Verification is based on 256 outputs.

Accuracy of Different Searches

Figure 2: Accuracy of different searches on MATH and SciBench with varied sampling budget.

Table 4: Overall performance comparison with representative models on SciBench.

Detailed Inferred Examples using ReST-MCTS*

Reference

If you find our work helpful, please kindly cite our paper:

@article{zhang2024rest,
        title={ReST-MCTS*: LLM Self-Training via Process Reward Guided Tree Search},
        author={Zhang, Dan and Zhoubian, Sining and Yue, Yisong and Dong, Yuxiao and Tang, Jie},
        journal={arXiv preprint arXiv:2406.03816},
        year={2024}
      }